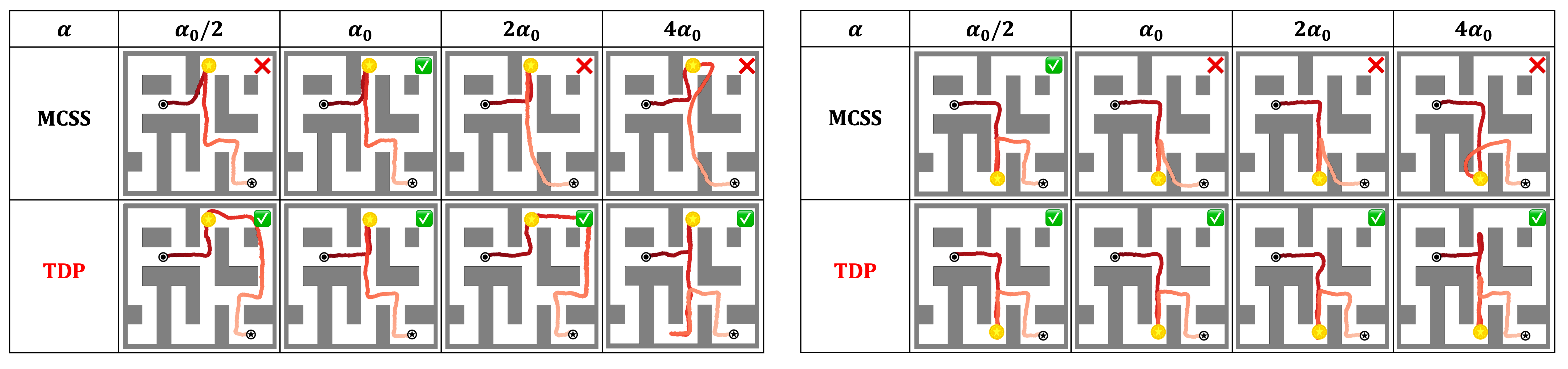
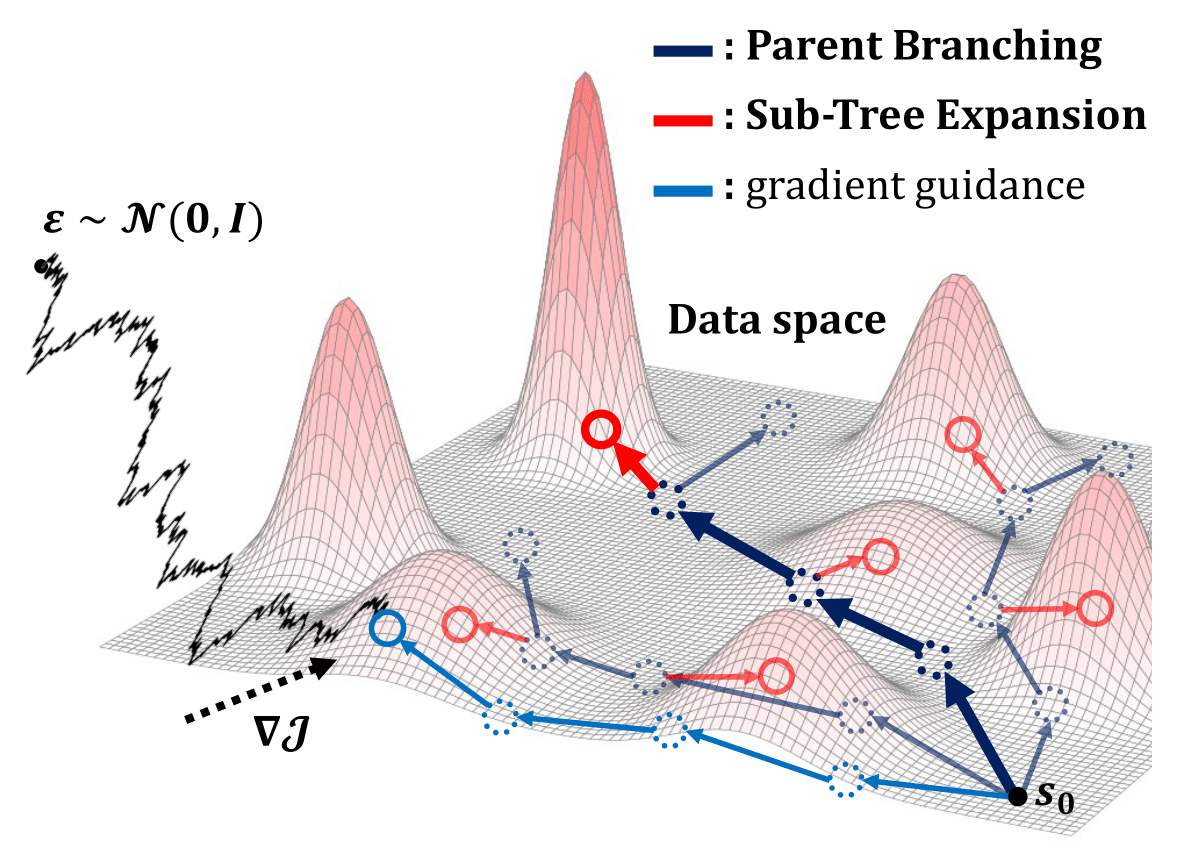
Parent Branching
Unlike conventional gradient guidance methods that pull samples toward high-reward regions, PG introduces repulsive forces that push samples apart in the data space. This leads to broad coverage of dynamically feasible trajectories independent of task objectives.
A single denoising step for parent branching denoted as:
$$
\left[\boldsymbol{\mu}^{i}_{\text{control}},\; \boldsymbol{\mu}^{i}_{\text{obs}}\right] \leftarrow \mathbf{SD}(\mathcal{J}, \boldsymbol{\mu}_{\theta}(\boldsymbol{\tau}^{i}))
$$
$$
\boldsymbol{\mu}^{i-1}_{\text{control}} \leftarrow \boldsymbol{\mu}^{i}_{\text{control}} + \alpha_p \Sigma^i \nabla \Phi(\boldsymbol{\mu}^{i}_{\text{control}}), \quad
\boldsymbol{\mu}^{i-1}_{\text{obs}} \leftarrow \boldsymbol{\mu}^{i}_{\text{obs}} + \alpha_g \Sigma^i \nabla \mathcal{J}(\boldsymbol{\mu}^{i}_{\text{obs}})
$$
$$
\boldsymbol{\mu}^{i-1} \leftarrow \left[\boldsymbol{\mu}^{i-1}_{\text{control}},\; \boldsymbol{\mu}^{i-1}_{\text{obs}}\right]
$$
$$
\boldsymbol{\tau}^{i-1} \sim \mathcal{N}(\boldsymbol{\mu}^{i-1}, \Sigma^i)
$$
where $\boldsymbol{\mu}^i_{\text{control}}$ and $\boldsymbol{\mu}^i_{\text{obs}}$ denote the
control and
observation components of the predicted mean of the denoising trajectory at timestep $i$, and $(\alpha_p, \alpha_g)$ are the guidance strengths for the particle guidance and gradient guidance, respectively.
$\mathbf{SD}(\mathcal{J}, \cdot)$ is the state decomposition function that autonomously partitions the state vector into
control and
observation components based on the test-time task $\mathcal{J}$, while $\Phi(\cdot)$ denotes the radical basis function (RBF) kernel in particle guidance.
Sub-Tree Expansion
For each parent trajectory, a random branch site is selected, and a child trajectory is generated by denoising from a partially noised version of the parent trajectory in order to refine parent trajectories using gradient guidance signals. Sub-tree expansion proceeds as:
$$
\boldsymbol{\tau}_{\text{child}}^{N_f} \sim q_{N_f}(\boldsymbol{\tau}_{\text{parent}}, \boldsymbol{C}) \quad
\text{where} \; \boldsymbol{C}=\{ \boldsymbol{s}_k \}_{k=0}^{b} \; \text{and} \; b\sim Uniform\left(0, T_{\text{pred}}\right)
$$
where $\boldsymbol{C}$ denotes the parent trajectory prefix, $q_{N_f}$ is the partial forward noising distribution with $N_f$ denoising steps, and $\boldsymbol{\tau}_{\text{child}}^{N_f}$ is the partially noised trajectory from which the child trajectory is denoised during sub-tree expansion.
The full algorithm of TDP  is provided in Algorithm.
is provided in Algorithm.
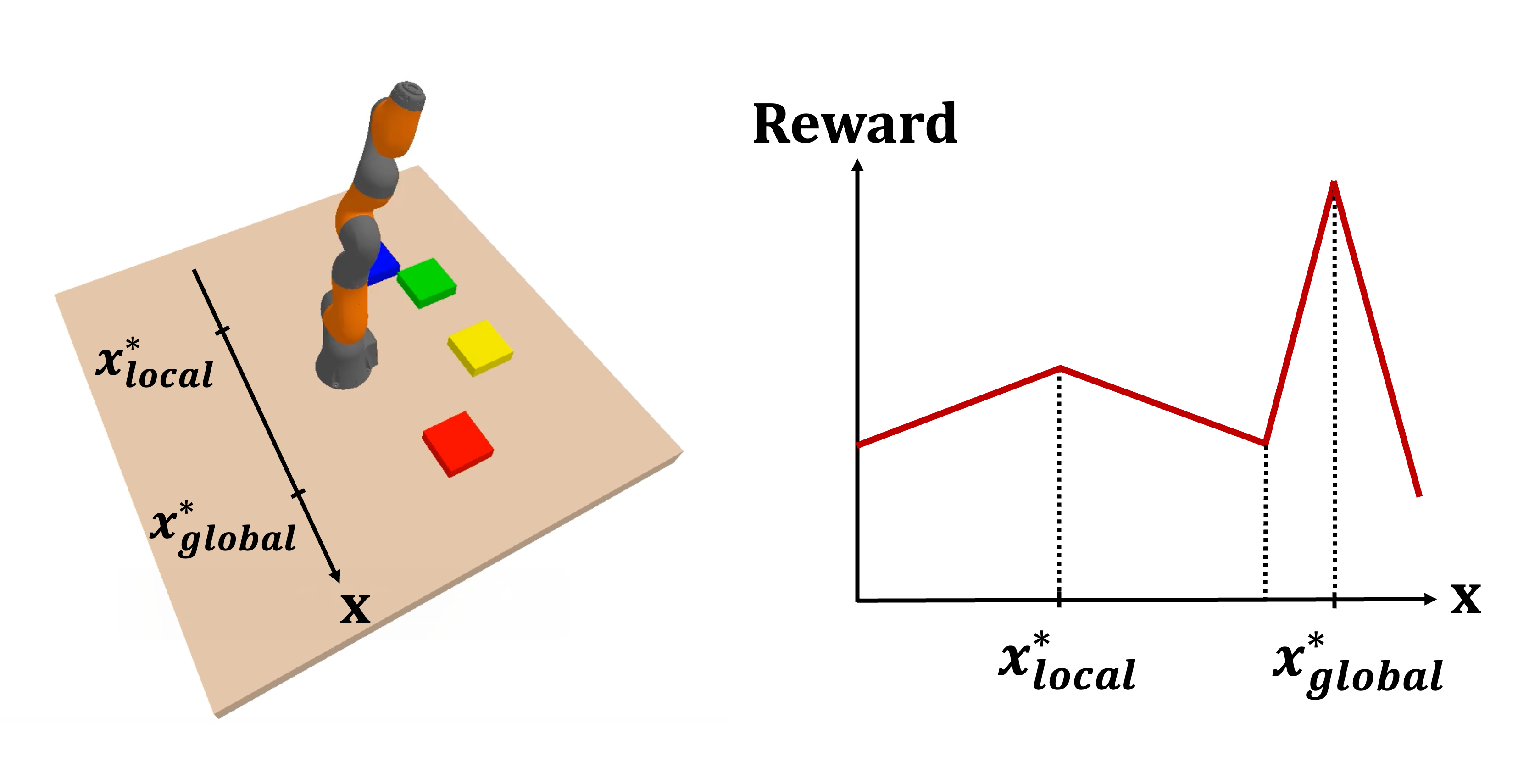
 is a zero-shot test-time planning framework that balances exploration and exploitation through structured trajectory generation.
It addresses the limitations of gradient guidance by exploring diverse trajectory regions and harnessing gradient information across this expanded solution space using only pretrained models and test-time reward signals.
is a zero-shot test-time planning framework that balances exploration and exploitation through structured trajectory generation.
It addresses the limitations of gradient guidance by exploring diverse trajectory regions and harnessing gradient information across this expanded solution space using only pretrained models and test-time reward signals.
 ).
).